A Novel CNN-Based Poisson Solver for Fluid Simulation

Abstract

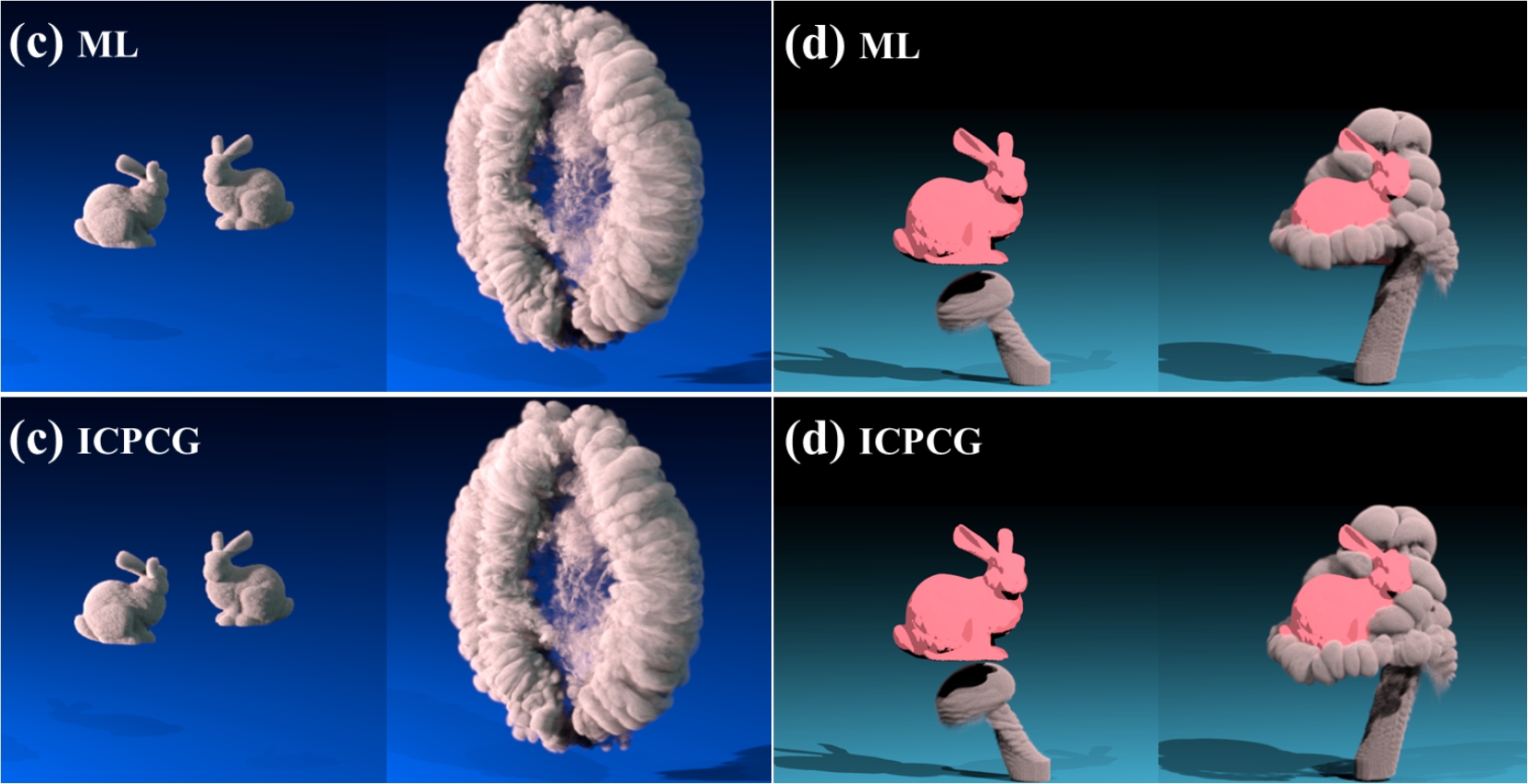
Solving a large-scale Poisson system is computationally expensive for most of the Eulerian fluid simulation applications. We propose a novel machine learning-based approach to accelerate this process. At the heart of our approach is a deep convolutional neural network (CNN), with the capability of predicting the solution (pressure) of a Poisson system given the discretization structure and the intermediate velocities as input. Our system consists of four main components, namely, a deep neural network to solve the large linear equations, a geometric structure to describe the spatial hierarchies of the input vector, a Principal Component Analysis (PCA) process to reduce the dimension of input in training, and a novel loss function to control the incompressibility constraint. We have demonstrated the efficacy of our approach by simulating a variety of high-resolution smoke and liquid phenomena. In particular, we have shown that our approach accelerates the projection step in a conventional Eulerian fluid simulator by two orders of magnitude. In addition, we have also demonstrated the generality of our approach by producing a diversity of animations deviating from the original datasets.

Links

[DOI]

Bibtex

@article{8478400,
  author={Xiao, Xiangyun and Zhou, Yanqing and Wang, Hui and Yang, Xubo},
  journal={IEEE Transactions on Visualization and Computer Graphics}, 
  title={A Novel CNN-Based Poisson Solver for Fluid Simulation}, 
  year={2020},
  volume={26},
  number={3},
  pages={1454-1465},
  doi={10.1109/TVCG.2018.2873375}
}