A Two-Way Coupling Approach for Simulating Bouncing Droplets
A two-way coupling cut-cell approach to simulate bouncing droplet phenomena by incorporating the lubricated thin aerodynamic gap between fluid volumes

Abstract
This paper presents a two-way coupling approach to simulate bouncing droplet phenomena by incorporating the lubricated thin aerodynamic gap between fluid volumes. At the heart of our framework lies a cut-cell representation of the thin air film between colliding liquid fluid volumes. The air pressures within the thin film, modeled using a reduced fluid model based on the lubrication theory, are coupled with the volumetric liquid pressures by the gradient across the liquid-air interfaces and solved in a monolithic two-way coupling system. Our method can accurately solve liquid-liquid interaction with air films without adaptive grid refinements, enabling accurate simulation of many novel surface-tension-driven phenomena such as droplet collisions, bouncing droplets, and promenading pairs.
Video
Overview
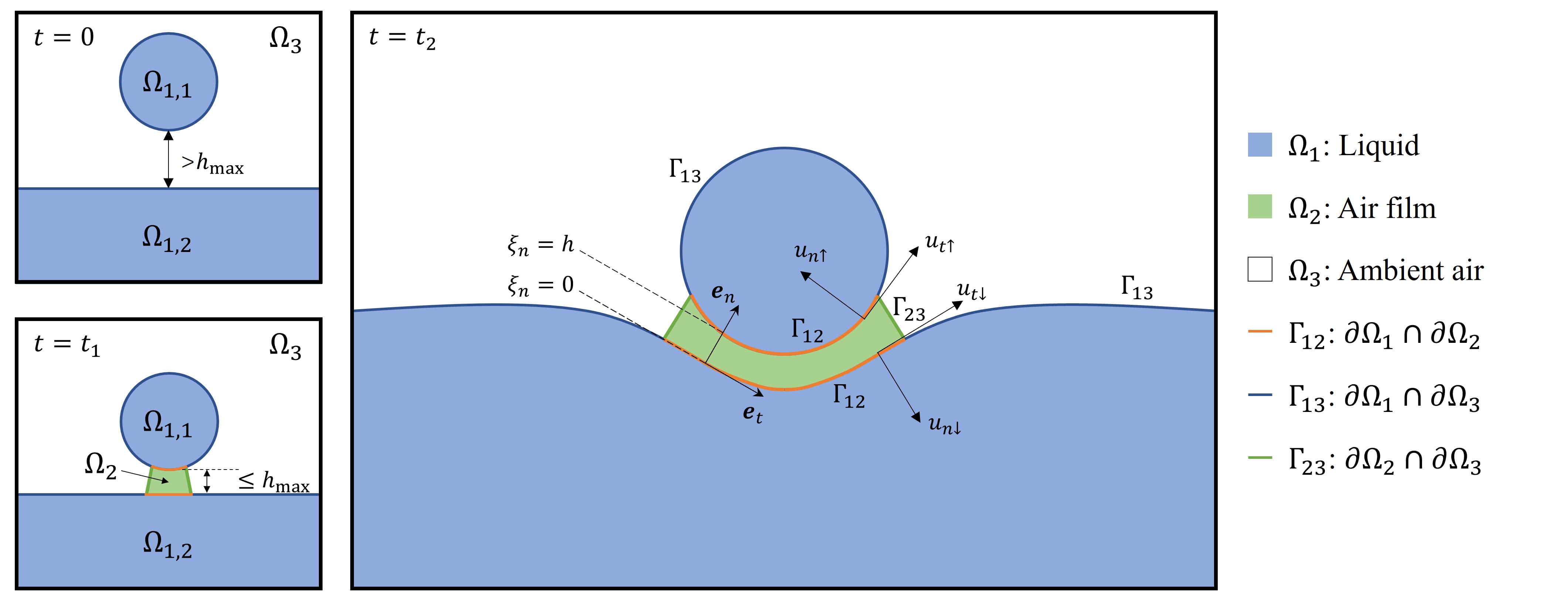
Illustration of fluid domains and interfaces
The entire computational domain is divided into three domains. \(\Omega_1\) is liquid, \(\Omega_2\) is the thin air film, and \(\Omega_3\) is ambient air. We show examples of the domain evolution at \(t = \{0, t_1, t_2\}\).
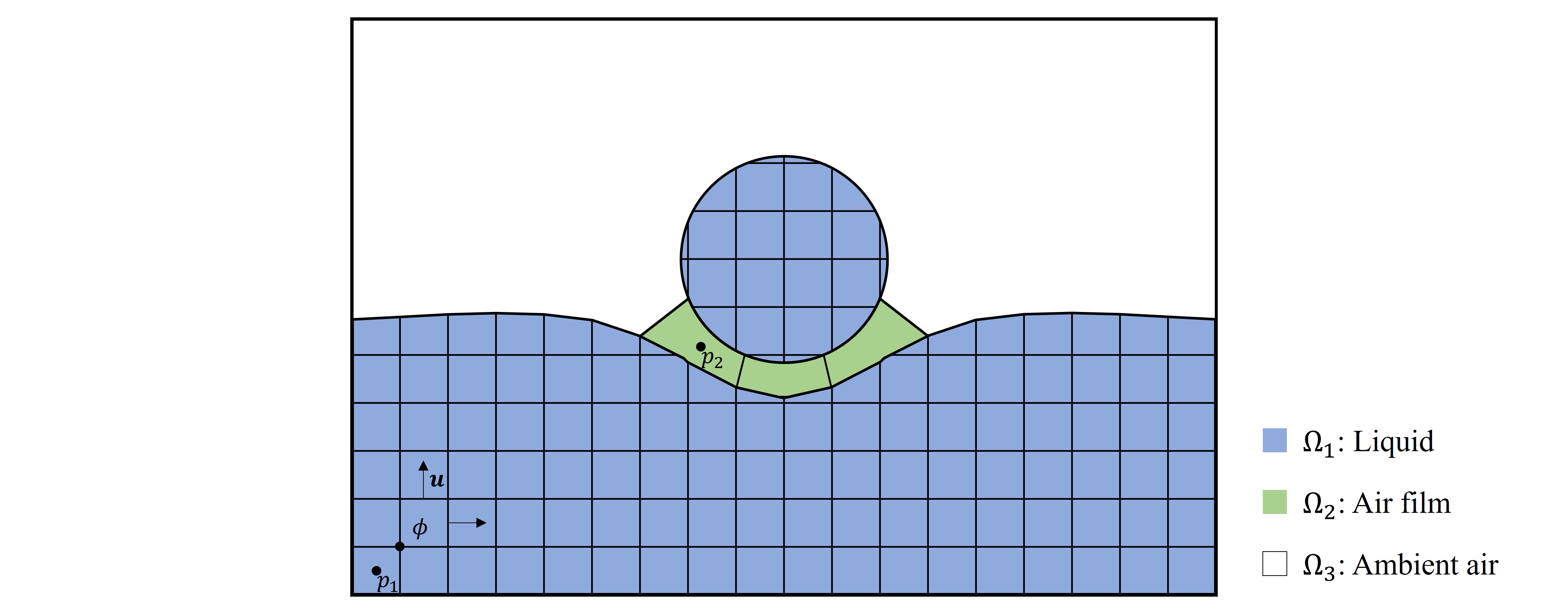
Discretization of liquids and the air film
The liquid domain \(\Omega_1\) (blue) is divided into several separate liquid volumes on the Cartesian grid enhanced by cut-cells, with level set \(\phi\), pressure \(p_1\) and velocity \(u\) sampled on nodes, cells, and faces. In the gap between liquid volumes, the air film \(\Omega_2\) (green) is represented by single-layered irregular cells and the cut-cell meshes to solve pressure \(p_2\).
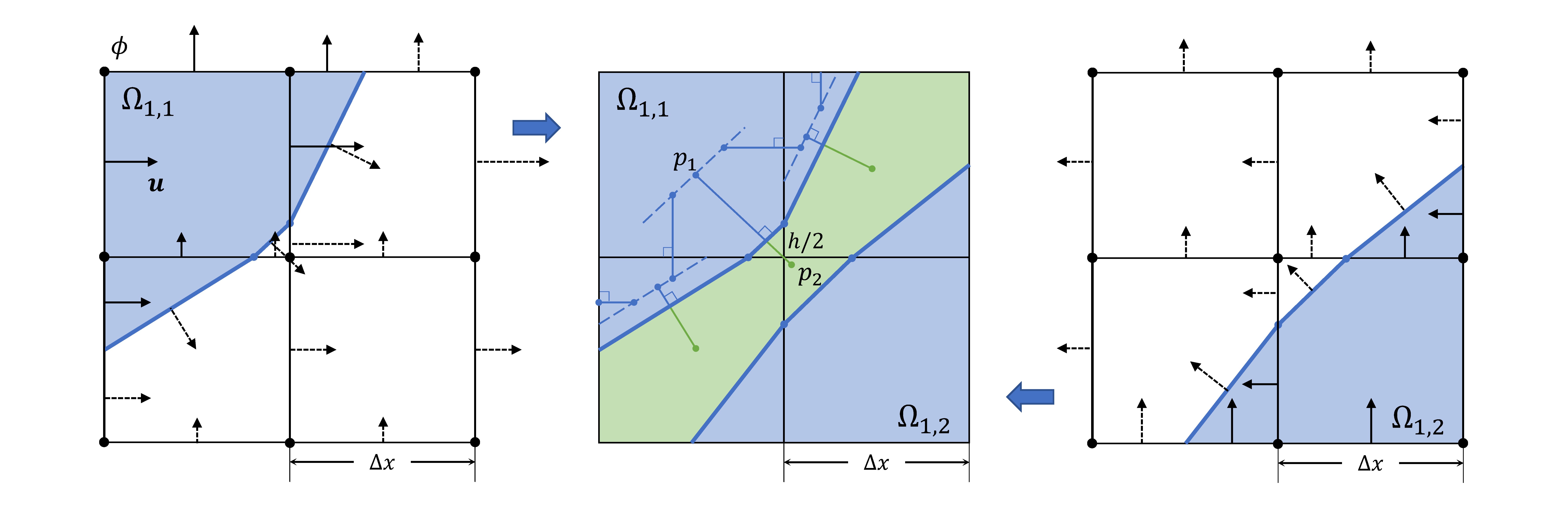
Discretization of the liquid level set, velocity, and pressure
We split the liquid domain into multiple liquid regions \((\Omega_{1,1}, \Omega_{1,2}, ...)\). Left and Right: Each region has its own node-based level set \(\phi\) (black dots) and face-based velocity field \(u\) (solid arrows). The interfaces \(\partial\Omega_1\) are discretized into the cut-cell mesh (blue segments) by performing the marching cubes algorithm on level sets. The velocity fields are sampled on grid faces (solid arrows) and extrapolated (dashed arrows). Middle: When coupling fluid regions with the air film (green), the normal velocities on the cut faces (dashed arrows) are interpolated from the grid faces. The pressure samples (blue dots) in the cut-cell are repositioned on the same iso-distance (blue dotted lines) parallel to the interface, following [70].
Results
Binary droplet collision
Top and Bottom: Representative frames of the rendered images from our simulation and the experimental snapshots from [1]. Middle: The evolution of the \(x\)-axis positions of two droplets. The regions filled by the light color are the \(x\)-axis bounding box of two droplets. Solid lines denote the \(x\)-axis center position of two droplets.

A droplet bouncing on a vibrating bath in (2,1) mode
Top: Rendered images of four representative frames. Bottom: Temporal evolution of the scene. The solid line denotes the movement of the droplet center, and the dashed line denotes the bath movement.


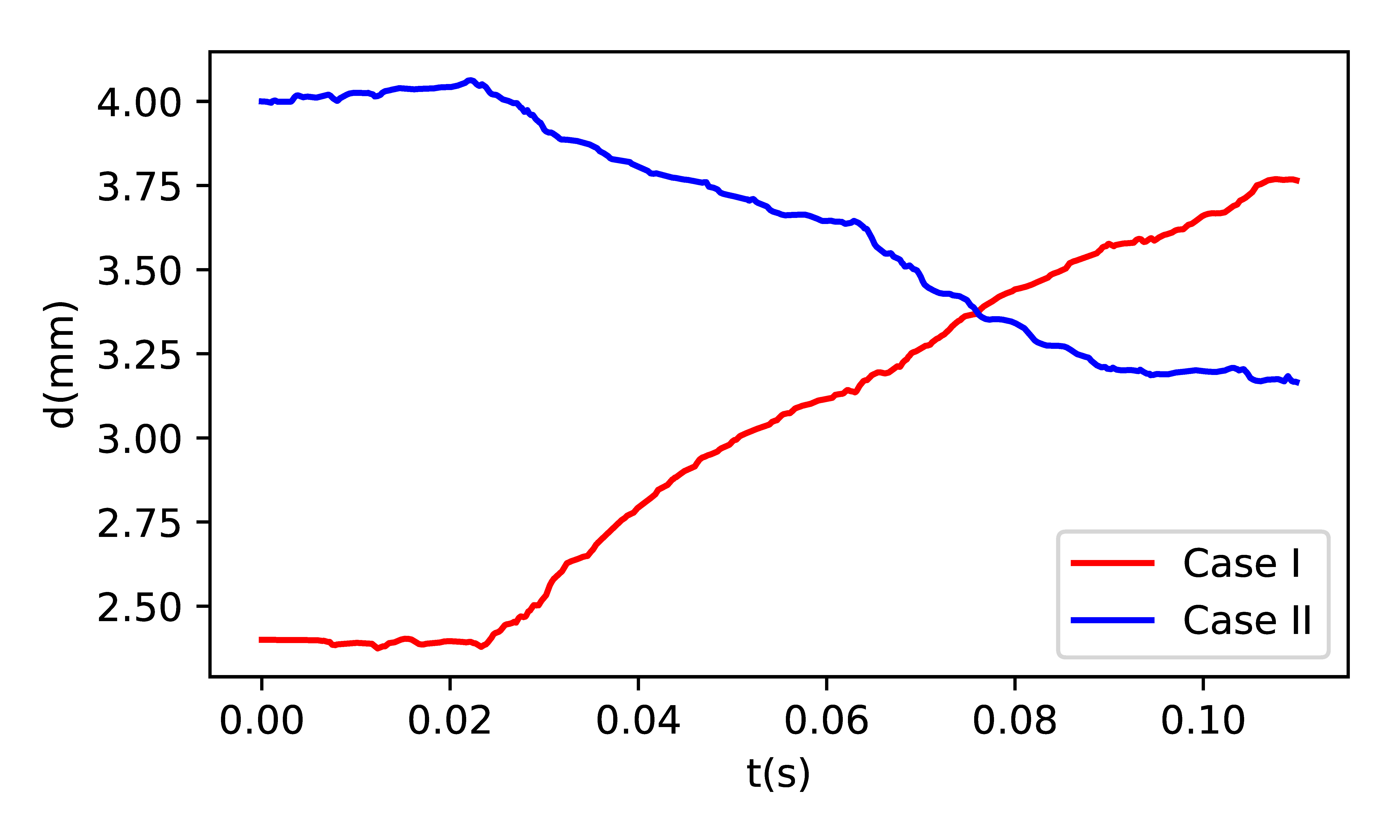
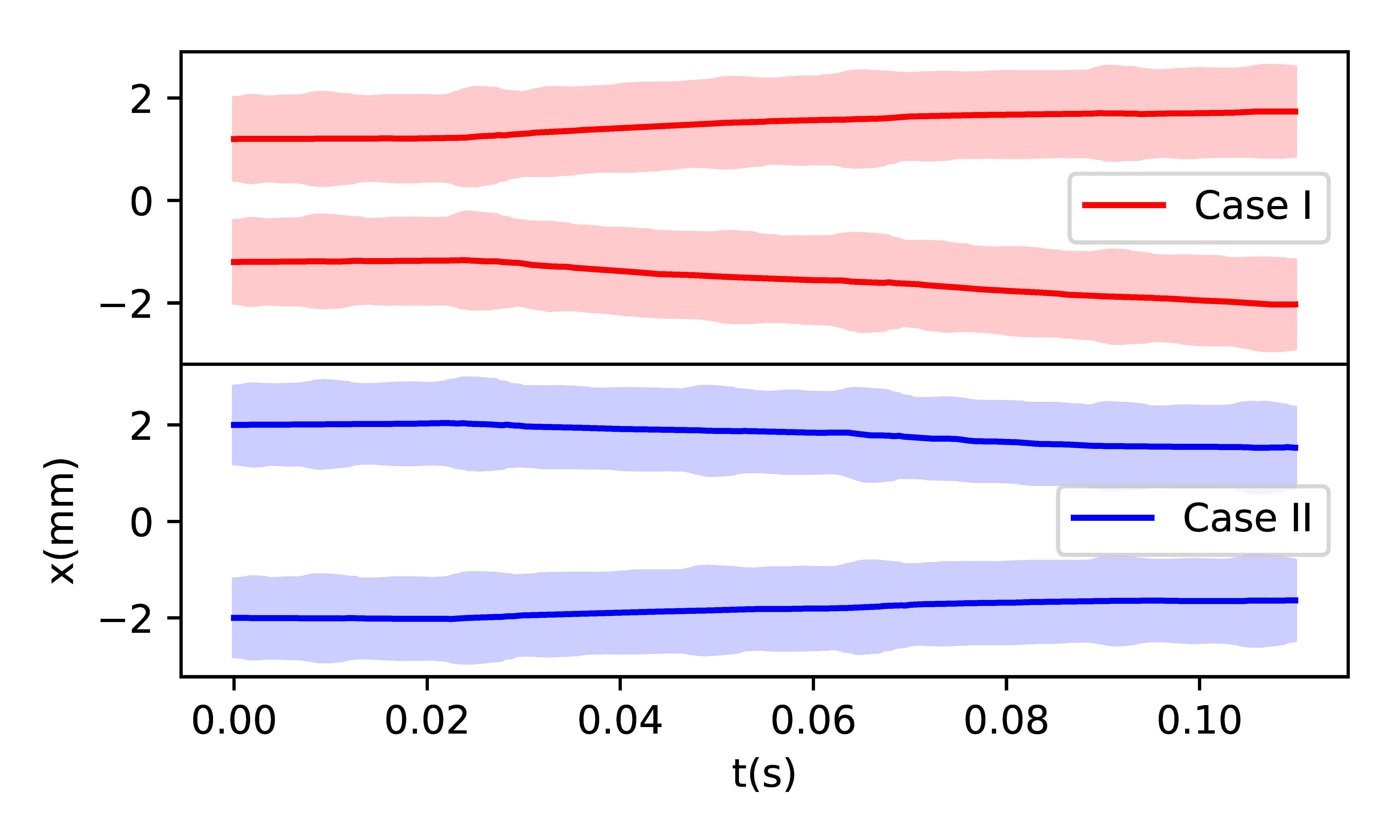
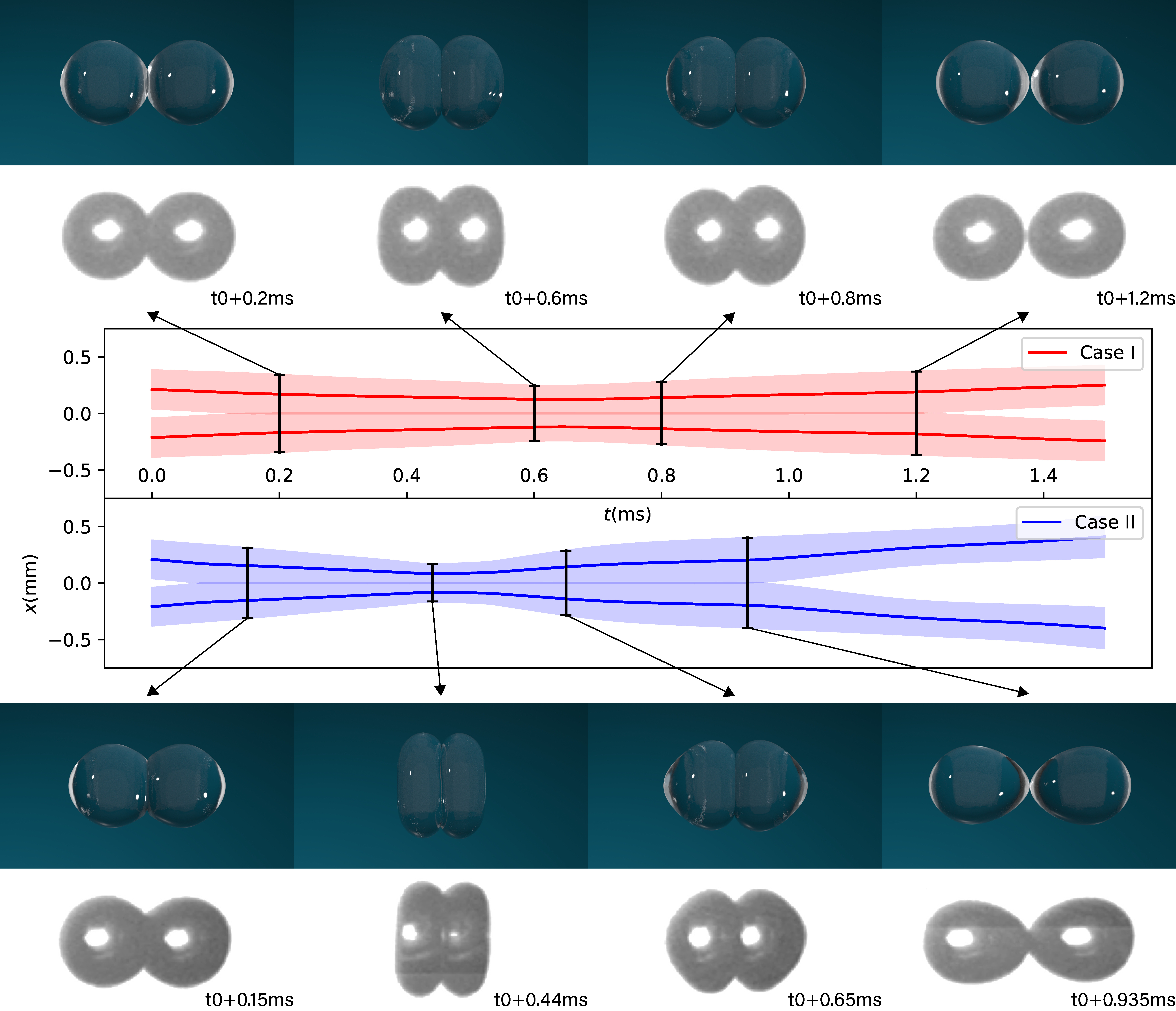
Promenading pairs
The two droplets bounce on the vibrating bath and form the promenading pairs. Left: Rendered result for Case I, where two droplets bounce and move away from each other. Middle: Rendered result for Case II, where the droplets move towards each other. Right top: The droplet positions as a function of time \(t\). The colored stripes indicate the \(x\)-axis bounding box of droplets. The solid lines represent the trajectories of the droplet centers. Right bottom: The droplet distances as a function of time \(t\).

Droplet merging and pinching
A large droplet falls and merges with the bath, which causes a thin liquid column to form due to the surface tension. The column eventually breaks off and pinches off a smaller droplet bouncing on the bath.
