A Moving Least-Squares/Level-Set Particle Method for Bubble and Foam Simulation
A novel particle-grid scheme for simulating intricate bubble and foam flow, with MLS particles serving as interfacial trackers and surfacial discretization, enables solving both volumetric air-liquid flow and surface surfactant flow simultaneously

Abstract
We present a novel particle-grid scheme for simulating bubble and foam flow. At the core of our approach lies a particle representation that combines the computational nature of moving least-squares particles and particle level-set methods. Specifically, we assign a dedicated particle system to each individual bubble, enabling accurate tracking of its interface evolution and topological changes in a foaming fluid system. The particles within each bubble’s particle system serve dual purposes. Firstly, they function as a surface discretization, allowing for the solution of surfactant flow physics on the bubble’s membrane. Additionally, these particles act as interface trackers, facilitating the evolution of the bubble’s shape and topology within the multiphase fluid domain. The combination of particle systems from all bubbles contributes to the generation of an unsigned level-set field, further enhancing the simulation of coupled multiphase flow dynamics. By seamlessly integrating our particle representation into a multiphase, volumetric flow solver, our method enables the simulation of a broad range of intricate bubble and foam phenomena. These phenomena exhibit highly dynamic and complex structural evolution, as well as interfacial flow details.
Method Overview
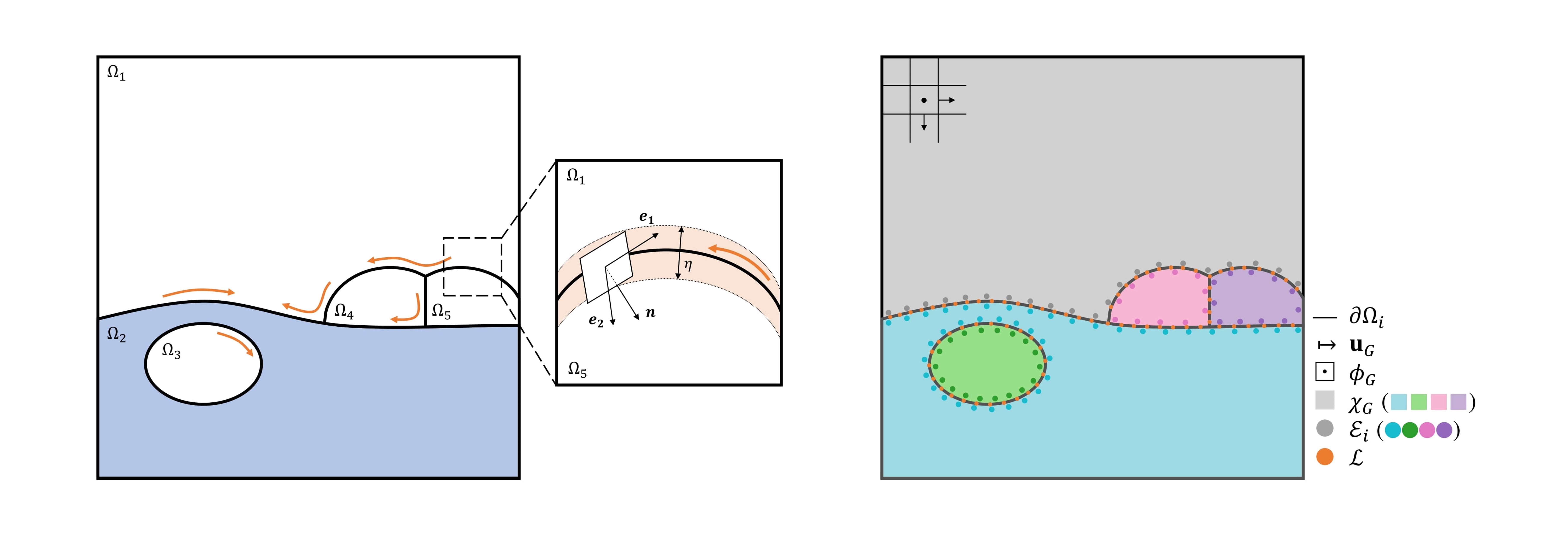
Illustration of domains
Left: The entire domain is divided into multiple volumetric regions \(\Omega_i\) and the their interfaces \(\partial \Omega_i\). The interfaces are treated as thin films, characterized by the local frame \(R = [{e}_1, {n}]\) in 2D (\(R = [{e}_1, {e}_2, {n}]\) in 3D) and thickness η, where the interfacial flow is solved. Right: The illustration of our MLSLS particle system. Our MLSLS particle system includes two major components: a set of MLSLS particles \(\mathcal{E}\) and a background grid \(\mathcal{G}\). (1) The particles \(\mathcal{E}\) are divided into multiple groups \(\mathcal{E}_i\) to track the surface of each region \(\Omega_i\). (2) On the background grid \(\mathcal{G}\), we represent the implicit surface with a indicator map \(\chi_\mathcal{G}\) and a global level set \(\phi_\mathcal{G}\). A velocity field \(u_\mathcal{G}\) is stored on the staggered grid. An extra set of Lagrangian particles \(\mathcal{L}\) is introduced on the interface to track the interfacial flow across different regions.
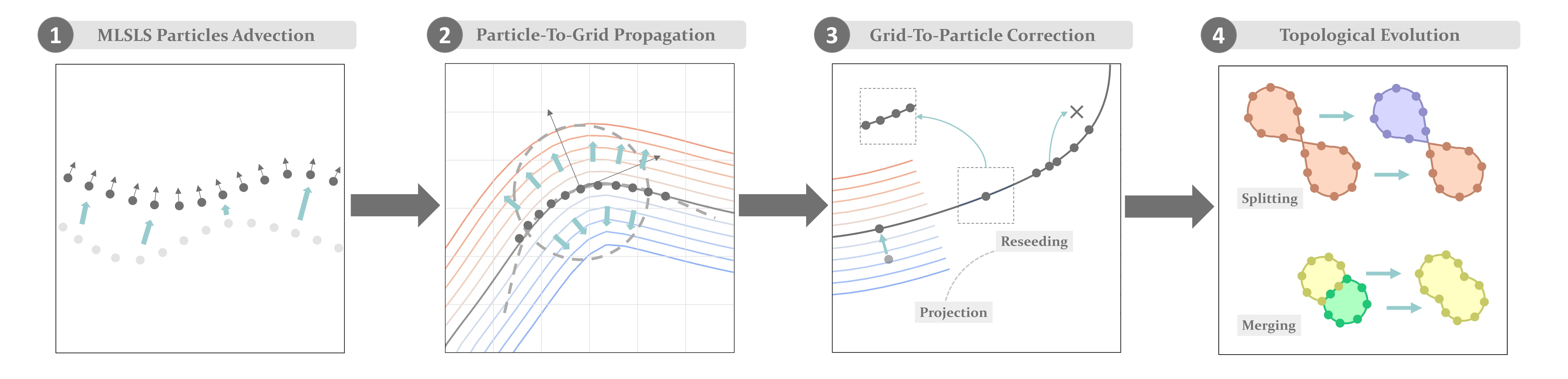
The process of geometric evolution of our MLSLS particles system
(1) Advect MLSLS particles \(\mathcal{E}\) using the velocity field \(u_\mathcal{G}\); (2) Reconstruct the level-set-based implicit interfaces on the grid \(\mathcal{G}\) using local MLS surfaces approximated on \(\mathcal{E}\); (3) Correct particles \(\mathcal{E}\) based on the grid \(\mathcal{G}\) to achieve consistent interface representation between grid and particle and a optimal distribution; (4) Handle topological changes between regions including splitting and merging.

The process of interfacial flow simulation
(1) Redistribute MLSLS particles \(\mathcal{E}\) within each region; (2) Transfer physical quantities from Lagrangian particles \(\mathcal{L}\) to MLSLS particles \(\mathcal{E}\) in their closest two regions; (3) Compute interfacial geometry; (4) Solve tangential dynamics within each region separately; (5) Transfer quantities from MLSLS particles \(\mathcal{E}\) to Lagrangian particles \(\mathcal{L}\).
Results
Jet on bubbles | Double bubbles




Bubble life | Multi-bubbles on water


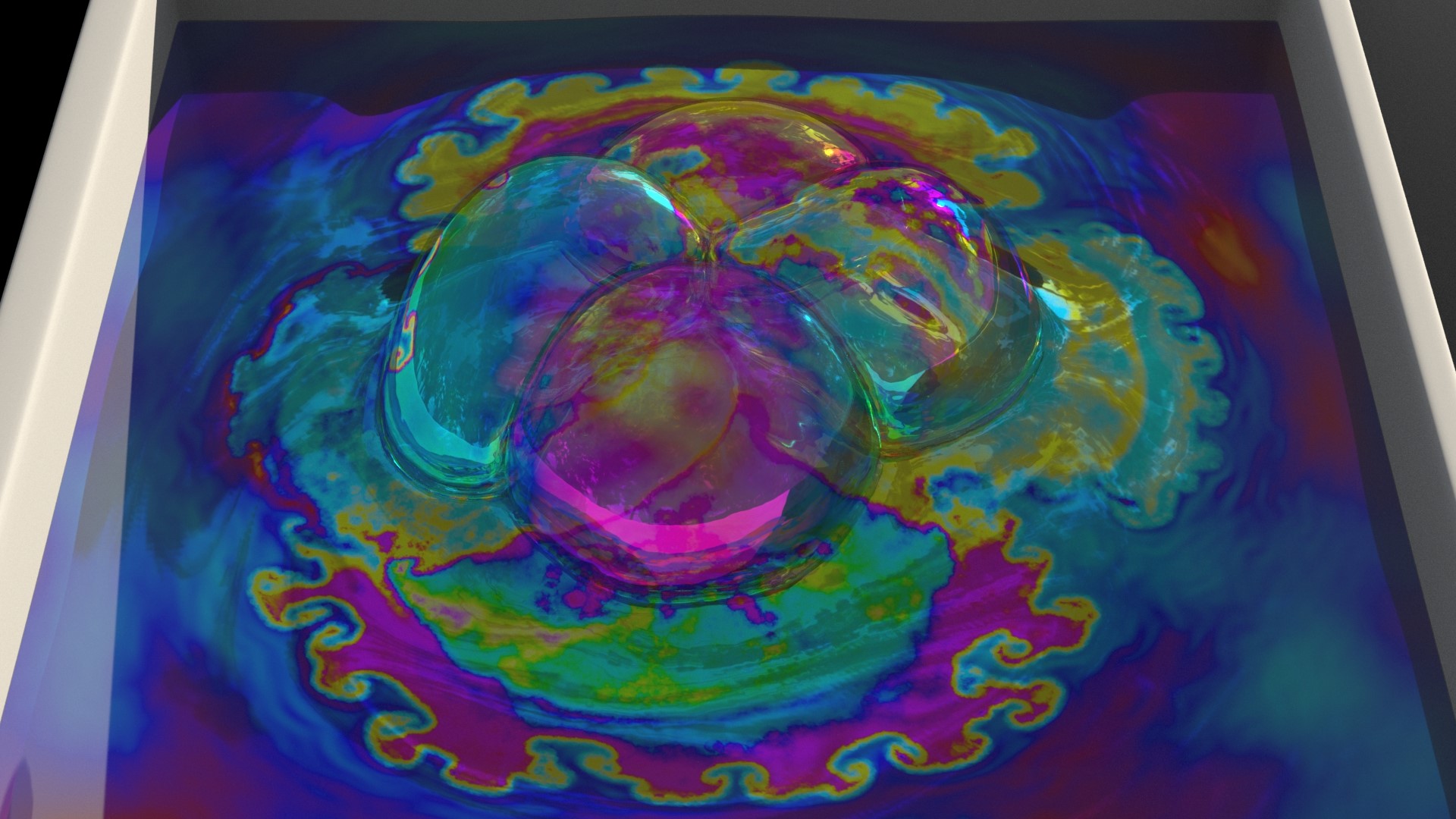

Four bubbles | Rising bubbles




Video
Links
[Preprint] [Preprint (Compressed)] [Preprint (Appendix)] [Slides for PG2024]
Bibtex
@articl{10536666,
author={Wang, Hui and Wang, Zhi and Hong, Shulin and Yang, Xubo and Zhu, Bo},
journal={IEEE Transactions on Visualization and Computer Graphics},
title={A Moving Least-Squares/Level-Set Particle Method for Bubble and Foam Simulation},
year={2024},
volume={},
number={},
pages={1-15},
keywords={Fluids;Surfactants;Surface tension;Mathematical models;Liquids;Level set;Geometry;Level set;interface tracking;particle methods;moving least-squares;multiphase fluid;surface tension},
doi={10.1109/TVCG.2024.3404151}
}
